Materialforschung
In seiner Biographie "Der Teil und das Ganze" berichtet Werner Heisenberg von Gesprächen in der Frühzeit der Quantenmechanik. Es herrschte allgemein Übereinstimmung, dass man nach der Erarbeitung der Grundregeln zum Verständnis des atomaren Aufbaus der Materie diese "nur" noch auf die Chemie und die Biologie anwenden müsse, um zu einem ähnlich grundlegenden Verständnis der Naturvorgänge zu gelangen wie in der Physik. Nun denn, fast 100 Jahre lang haben sich die Naturwissenschaften diesem Programm gewidmet und dabei überwältigende und inspirierende Einsichten in die Natur entdeckt. Aber wir sind noch nicht fertig - es gibt noch viel zu erforschen, um chemische und biologische Stoffe zu verstehen und um der von Heisenberg und Kollegen gehegten Hoffnung näher zu kommen.
Dünne Schichten
stehen im Fokus vieler materialwissenschaftlicher Studien und Anwendungen. Bei den meisten Beschichtungsprozessen werden dünne Schichten Atom für Atom auf ein Substrat abgeschieden. Es ist offensichtlich, dass die Physik und die Funktionalität der Schicht empfindlich von der relativen Anordnung der Atome, d. h. ihrer Struktur und Morphologie, abhängen. Die strukturbildenden Prozesse von dünnen Schichten lassen sich in (1) oberflächenbezogene und (2) volumenbezogene Prozesse unterteilen. Beide Prozesse bewirken eine ausgeprägte Vorzugsorientierung der Kristallite in polykristallinen Schichten und führen zu wachstumsbedingten Spannungsfeldern, die beide die angestrebte Schichtfunktionalität maßgeblich beeinflussen können. Die Wellenlängen der Röntgenstrahlung liegen in der gleichen Größenordnung wie typische interatomare Abstände, also im Bereich von 0,1 nm. Daher werden Röntgenstrahlen als effektive Sonde verwendet, um die lokale Struktur innerhalb dünner Schichten zu bestimmen (vergl. aktuelles Kapitel in ITC vol. H) und zu untersuchen
- chemische Phasen und Zusammensetzung
- Vorzugsorientierung der Kristallite (Textur)
- Korngrößen und Mikrospannungen
- mechanische Eigenspannungen
- thin film density and voids or void networks.
Mit diesen Daten verfügt der Dünnschichttechnologe über wichtige Informationen, um die Mechanismen aufzuklären, die die Schicht wachsen lassen, und um das Schichtwachstum so zu gestalten, dass die gewünschten Eigenschaften erzielt werden.
Kristallographie
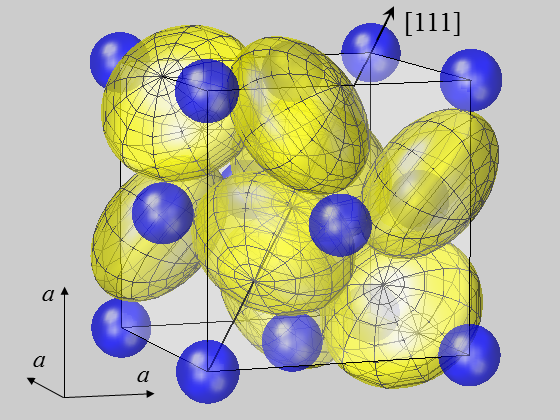
Bei der Berechnung von Kristalleigenschaften wird oft von einer kugelförmigen Modellierung der Atome auf ihren Kristallgitterplätzen ausgegangen. Doch die Frage ist: Sind Atome immer so rund wie eine Kugel? Streng genommen ist der Ansatz nur für Atome und Ionen auf Positionen hoher Symmetrie wie im fcc-Gitter oder der NaCl-Struktur gerechtfertigt. In den meisten Kristallstrukturen befinden sich die Atome jedoch auf Positionen geringerer Symmetrie, bei denen eine signifikante Abweichung der Elektronendichte von der Form einer Kugel auftreten kann.
Dies gilt für viele Kristalle, die in Hochtechnologie-Anwendungen wie Piezo- oder Ferroelektrika, High-k-Dielektrika, Photovoltaik und vielen anderen eingesetzt werden. Für Kristallbestandteile auf polaren Positionen (Punktgruppensymmetrie C1, Cs, Cn, Cnv, n = 2, 3, 4, 6) können induzierte Dipolmomente hervorgerufen werden [13], die für die Kristallenergie [9, 15], die Berechnung von Pyro- und Piezokonstanten [14] oder den optischen Absorptionskoeffizienten [11] von Bedeutung sind. Generell kann gesagt werden, dass Atome an diesen Positionen eine Schlüsselfrage für das Verständnis anisotroper Kristalleigenschaften darstellen. Kürzlich wurde gezeigt, dass das Konzept der Ionenradien erweitert werden muss und dass Anionen zweckmäßigerweise durch Ellipsoide und nicht durch Kugeln modelliert werden sollten. Für die Fallstudien von Verbindungen vom Pyrit-Typ wurde gezeigt, dass ellipsoidische Verformungen für S-Ionen in Disulfiden MS2 [48] und, allgemeiner, für Chalcogen-Ionen X in Dichalcogeniden MX2 auftreten [62].